Learn it by examples

By David Kebo Houngninou

On this page, you will find some simple and practical examples of how to use CUDD.
Note: All Credits go to the author of the package, Fabio Somenzi at the Dept. of Electrical and Computer Engineering, University of Colorado at Boulder

What is CUDD?
Where to download CUDD?
How to install CUDD?
Tutorial 1: Write your first program with CUDD
How to debug your program
Visualize the BDD
Tutorial 2: BDD of Boolean functions
BDD for the Exclusive-OR Boolean function
BDD for the AND Boolean function
BDD for the OR Boolean function
BDD for the XNOR Boolean function
BDD for the NAND Boolean function
BDD for the NOR Boolean function
BDD for the NOT Boolean function
BDD for the function f = x0’x1’x2’x3′
Tutorial 3: Variable reordering
Tutorial 4: Additional functions
Algebraic Decision Diagram (ADD) for a fanout
Algebraic Decision Diagram (ADD) for a crossover

What is CUDD?

CUDD stands for Colorado University Decision Diagram. It is a package for the manipulation of Binary Decision Diagrams (BDDs), Algebraic Decision Diagrams (ADDs), and Zero-suppressed Binary Decision Diagrams (ZDDs).

Where to download CUDD?

cudd-3.0.0
cudd-2.5.1
cudd-2.5.0
cudd-2.4.2

These directories contain the decision diagram package and a few support libraries

How to install CUDD?

To build an application that uses the CUDD package, you should add:

#include "util.h"
#include "cudd.h"

to your source files, and should link libcudd.a , libmtr.a , libst.a , and libutil.a to your executable. (All these libraries are part of the distribution.) Some platforms require specific compiler and linker flags. Refer to the Makefile in the top-level directory of the distribution.

An example of a Makefile is the following: Makefile

Tutorial 1: Write your first program with CUDD

The basic use of CUDD is easy:

Initialize a DdManager using Cudd_Init
Create the DD
Shut down the DdManager using Cudd_Quit(DdManager* ddmanager)

Sample code for the main program

The program below creates a single BDD variable

int main (int argc, char *argv[])
{
    DdManager *gbm; /* Global BDD manager. */
    char filename[30];
    gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0); /* Initialize a new BDD manager. */
    DdNode *bdd = Cudd_bddNewVar(gbm); /*Create a new BDD variable*/
    Cudd_Ref(bdd); /*Increases the reference count of a node*/
    Cudd_Quit(gbm);
    return 0;
}

How to debug your program

One handy debugging tool in the CUDD package is a function called Cudd_PrintDebug()
Cudd_PrintDebug() takes as parameters the following (in the listed order):

DdManager* ddmanager; //The manager
DdNode* ddnode; //The Decision diagram
int n;
int pr; //The level of debugging

pr can be set from 0 to any number, depending on the amount of information you want to display.
This function prints out useful statistics including the number of nodes, the number of leaves, and the number of minterms.

Sample function for printing a DD summary

/**
 * Print a dd summary
 * pr = 0 : prints nothing
 * pr = 1 : prints counts of nodes and minterms
 * pr = 2 : prints counts + disjoint sum of product
 * pr = 3 : prints counts + list of nodes
 * pr > 3 : prints counts + disjoint sum of product + list of nodes
 * @param the dd node
 */
void print_dd (DdNode	*dd, int n, int pr, char *name)
{
    printf("%s\n", name);
    printf("DdManager nodes: %ld | ", Cudd_ReadNodeCount(gbm)); /*Reports the number of live nodes in BDDs and ADDs*/
    printf("DdManager vars: %d | ", Cudd_ReadSize(gbm) ); /*Returns the number of BDD variables in existance*/
    printf("DdNode nodes: %d | ", Cudd_DagSize(dd)); /*Reports the number of nodes in the BDD*/
	printf("DdNode vars: %d | ", Cudd_SupportSize(gbm, dd) ); /*Returns the number of variables in the BDD*/
    printf("DdManager reorderings: %d | ", Cudd_ReadReorderings(gbm) ); /*Returns the number of times reordering has occurred*/
    printf("DdManager memory: %ld |\n\n", Cudd_ReadMemoryInUse(gbm) ); /*Returns the memory in use by the manager measured in bytes*/
    Cudd_PrintDebug(gbm, dd, n, pr);	// Prints to the standard output a DD and its statistics: number of nodes, number of leaves, number of minterms.
}

Another handy function is Cudd_PrintInfo()
Cudd_PrintInfo() prints out statistics and settings for a CUDD manager:
You can get a lot of useful information from Cudd_PrintInfo(). The lines below show the statistics dumped to a file:

**** CUDD modifiable parameters ****
Hard limit for cache size: 699050
Cache hit threshold for resizing: 30%
Garbage collection enabled: yes
Limit for fast unique table growth: 419430
Maximum number of variables sifted per reordering: 1000
Maximum number of variable swaps per reordering: 2000000
Maximum growth while sifting a variable: 1.2
Dynamic reordering of BDDs enabled: no
Default BDD reordering method: 4
Dynamic reordering of ZDDs enabled: no
Default ZDD reordering method: 4
Realignment of ZDDs to BDDs enabled: no
Realignment of BDDs to ZDDs enabled: no
Dead nodes counted in triggering reordering: no
Group checking criterion: 7
Recombination threshold: 0
Symmetry violation threshold: 0
Arc violation threshold: 0
GA population size: 0
Number of crossovers for GA: 0
Next reordering threshold: 4004
**** CUDD non-modifiable parameters ****
Memory in use: 8949888
Peak number of nodes: 1022
Peak number of live nodes: 19
Number of BDD variables: 4
Number of ZDD variables: 0
Number of cache entries: 262144
Number of cache look-ups: 12
Number of cache hits: 0
Number of cache insertions: 14
Number of cache collisions: 0
Number of cache deletions: 0
Cache used slots = 0.01% (expected 0.01%)
Soft limit for cache size: 5120
Number of buckets in unique table: 1280
Used buckets in unique table: 1.80% (expected 1.78%)
Number of BDD and ADD nodes: 23
Number of ZDD nodes: 0
Number of dead BDD and ADD nodes: 8
Number of dead ZDD nodes: 0
Total number of nodes allocated: 23
Total number of nodes reclaimed: 0
Garbage collections so far: 0
Time for garbage collection: 0.00 sec
Reorderings so far: 0
Time for reordering: 0.00 sec

Visualize the BDD

So, you successfully created a BDD, now what?

After you create a BDD or an ADD of type DdNode, you can plot it as a .dot file using the Cudd_DumpDot() function. You should provide an output file pointer, the DD manager, the number of nodes, and the node array pointer. The following functions show how to print a DD to a file.

Here is a simple way to visualize the BDD as an actual graph.

Sample function for printing a dd summary

/**
 * Writes a dot file representing the argument DDs
 * @param the node object
 */
void write_dd (DdNode *dd, char* filename)
{
    FILE *outfile; // output file pointer for .dot file
    outfile = fopen(filename,"w");
    DdNode **ddnodearray = (DdNode**)malloc(sizeof(DdNode*)); // initialize the function array
    ddnodearray[0] = dd;
    Cudd_DumpDot(gbm, 1, ddnodearray, NULL, NULL, outfile); // dump the function to .dot file
    free(ddnodearray);
    fclose (outfile); // close the file */
}

Once you generate the .dot file, you can open it using the GraphViz tool.
Graphviz is open-source graph visualization software. It works very well for representing structural information as diagrams of abstract graphs and networks. GraphViz is available for download here: https://www.graphviz.org/download/.
Just locate the .dot file and open it with Graphviz.

Sample program for printing a creating and printing a dd (Complete)

The entire program looks like this

/*
* FILENAME: transfer.c
* Overview: BDD tutorial
* AUTHOR: David Kebo Houngninou
*/

#include <sys/types.h>
#include <sys/time.h>
#include <stdio.h>
#include <string.h>
#include <time.h>
#include <math.h>
#include <stdlib.h>
#include "cudd.h"

/**
 * Print a dd summary
 * pr = 0 : prints nothing
 * pr = 1 : prints counts of nodes and minterms
 * pr = 2 : prints counts + disjoint sum of product
 * pr = 3 : prints counts + list of nodes
 * pr > 3 : prints counts + disjoint sum of product + list of nodes
 * @param the dd node
 */
void print_dd (DdManager *gbm, DdNode *dd, int n, int pr )
{
    printf("DdManager nodes: %ld | ", Cudd_ReadNodeCount(gbm)); /*Reports the number of live nodes in BDDs and ADDs*/
    printf("DdManager vars: %d | ", Cudd_ReadSize(gbm) ); /*Returns the number of BDD variables in existence*/
    printf("DdManager reorderings: %d | ", Cudd_ReadReorderings(gbm) ); /*Returns the number of times reordering has occurred*/
    printf("DdManager memory: %ld \n", Cudd_ReadMemoryInUse(gbm) ); /*Returns the memory in use by the manager measured in bytes*/
    Cudd_PrintDebug(gbm, dd, n, pr);  // Prints to the standard output a DD and its statistics: number of nodes, number of leaves, number of minterms.
}


/**
 * Writes a dot file representing the argument DDs
 * @param the node object
 */
void write_dd (DdManager *gbm, DdNode *dd, char* filename)
{
    FILE *outfile; // output file pointer for .dot file
    outfile = fopen(filename,"w");
    DdNode **ddnodearray = (DdNode**)malloc(sizeof(DdNode*)); // initialize the function array
    ddnodearray[0] = dd;
    Cudd_DumpDot(gbm, 1, ddnodearray, NULL, NULL, outfile); // dump the function to .dot file
    free(ddnodearray);
    fclose (outfile); // close the file */
}

// This program creates a single BDD variable
int main (int argc, char *argv[])
{
    DdManager *gbm; /* Global BDD manager. */
    char filename[30];
    gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0); /* Initialize a new BDD manager. */
    DdNode *bdd = Cudd_bddNewVar(gbm); /*Create a new BDD variable*/
    Cudd_Ref(bdd); /*Increases the reference count of a node*/
    bdd = Cudd_BddToAdd(gbm, bdd); /*Convert BDD to ADD for display purpose*/
    print_dd (gbm, bdd, 2,4); /*Print the dd to standard output*/
    sprintf(filename, "./bdd/graph.dot"); /*Write .dot filename to a string*/
    write_dd(gbm, bdd, filename);  /*Write the resulting cascade dd to a file*/
    Cudd_Quit(gbm);
    return 0;
}

Graph representation of the BDD

Using Graphviz, you can visualize the BDD as a graph. The graph should look like this.

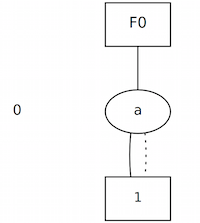
Download Tutorial 1

You can download the full code for this example here:

tutorial1.tar.gz

Tutorial 2: BDD of Boolean functions

Common manipulations of BDDs can be accomplished by calling operators on variables.
The CUDD package includes Boolean functions that can be used for BDD operations such as Cudd_Not, Cudd_bddAnd, Cudd_bddOr, Cudd_Xor, etc.

BDD for the Exclusive-OR Boolean function

The truth table for an Exclusive-OR

x1	x2	f
0	0	0
0	1	1
1	0	1
1	1	0

Logic gate for an Exclusive-OR

BDD for an Exclusive-OR

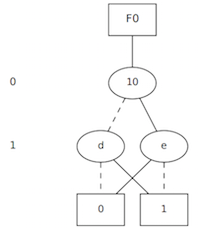
For the Exclusive-OR Boolean function, we use Cudd_bddXor
The following fragment of code illustrates how to build the BDD for the function f = x1 ⊕ x2

Sample program for the XOR Boolean function

The main function looks like this

int main (int argc, char *argv[])
{
    char filename[30];
    DdManager *gbm; /* Global BDD manager. */
    gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0); /* Initialize a new BDD manager. */
    DdNode *bdd, *x1, *x2;
    x1 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x1*/
    x2 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x2*/
    bdd = Cudd_bddXor(gbm, x1, x2); /*Perform XOR Boolean operation*/
    Cudd_Ref(bdd);          /*Update the reference count for the node just created.*/
    bdd = Cudd_BddToAdd(gbm, bdd); /*Convert BDD to ADD for display purpose*/
    print_dd (gbm, bdd, 2,4);   /*Print the dd to standard output*/
    sprintf(filename, "./bdd/graph.dot"); /*Write .dot filename to a string*/
    write_dd(gbm, bdd, filename);  /*Write the resulting cascade dd to a file*/
    Cudd_Quit(gbm);
    return 0; 
}

BDD for the AND Boolean function

The truth table for an AND

x1	x2	f
0	0	0
0	1	0
1	0	0
1	1	1

Logic gate for a logic AND

BDD for a logic AND

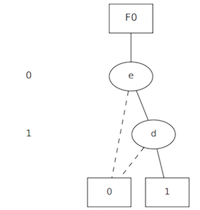
For the AND Boolean function, we use Cudd_bddAnd
The following fragment of code illustrates how to build the BDD for the function f = x1 ∧ x1

Sample program for the AND Boolean function

The main function looks like this

int main (int argc, char *argv[])
{
    char filename[30];
    DdManager *gbm; /* Global BDD manager. */
    gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0); /* Initialize a new BDD manager. */
    DdNode *bdd, *x1, *x2;
    x1 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x1*/
    x2 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x2*/
    bdd = Cudd_bddAnd(gbm, x1, x2); /*Perform AND Boolean operation*/
    Cudd_Ref(bdd);          /*Update the reference count for the node just created.*/
    bdd = Cudd_BddToAdd(gbm, bdd); /*Convert BDD to ADD for display purpose*/
    print_dd (gbm, bdd, 2,4);   /*Print the dd to standard output*/
    sprintf(filename, "./bdd/graph.dot"); /*Write .dot filename to a string*/
    write_dd(gbm, bdd, filename);  /*Write the resulting cascade dd to a file*/
    Cudd_Quit(gbm);
    return 0; 
}

BDD for the OR Boolean function

The truth table for a logic OR

x1	x2	f
0	0	0
0	1	1
1	0	1
1	1	1

Logic gate for a logic OR

BDD for a logic OR

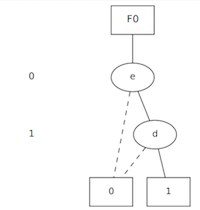
For the OR Boolean function, we use Cudd_bddOr
The following fragment of code illustrates how to build the BDD for the function f = x1 ∨ x2

Sample program for the OR Boolean function

The main function looks like this

int main (int argc, char *argv[])
{
    char filename[30];
    DdManager *gbm; /* Global BDD manager. */
    gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0); /* Initialize a new BDD manager. */
    DdNode *bdd, *x1, *x2;
    x1 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x1*/
    x2 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x2*/
    bdd = Cudd_bddOr(gbm, x1, x2); /*Perform OR Boolean operation*/
    Cudd_Ref(bdd);          /*Update the reference count for the node just created.*/
    bdd = Cudd_BddToAdd(gbm, bdd); /*Convert BDD to ADD for display purpose*/
    print_dd (gbm, bdd, 2,4);   /*Print the dd to standard output*/
    sprintf(filename, "./bdd/graph.dot"); /*Write .dot filename to a string*/
    write_dd(gbm, bdd, filename);  /*Write the resulting cascade dd to a file*/
    Cudd_Quit(gbm);
    return 0; 
}

BDD for the XNOR Boolean function

The truth table for an XNOR

x1	x2	f
0	0	1
0	1	0
1	0	0
1	1	1

Logic gate for an XNOR

BDD for an XNOR

For the XNOR Boolean function, we use Cudd_bddXnor
The following fragment of code illustrates how to build the BDD for the function f = ¬ (x1 ⊕ x2)

Sample program for the XNOR Boolean function

The main function looks like this

int main (int argc, char *argv[])
{
    char filename[30];
    DdManager *gbm; /* Global BDD manager. */
    gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0); /* Initialize a new BDD manager. */
    DdNode *bdd, *x1, *x2;
    x1 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x1*/
    x2 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x2*/
    bdd = Cudd_bddXnor(gbm, x1, x2); /*Perform XNOR Boolean operation*/
    Cudd_Ref(bdd);          /*Update the reference count for the node just created.*/
    bdd = Cudd_BddToAdd(gbm, bdd); /*Convert BDD to ADD for display purpose*/
    print_dd (gbm, bdd, 2,4);   /*Print the dd to standard output*/
    sprintf(filename, "./bdd/graph.dot"); /*Write .dot filename to a string*/
    write_dd(gbm, bdd, filename);  /*Write the resulting cascade dd to a file*/
    Cudd_Quit(gbm);
    return 0; 
}

BDD for the NAND Boolean function

The truth table for an NAND

x1	x2	f
0	0	1
0	1	1
1	0	1
1	1	0

Logic gate for an NAND

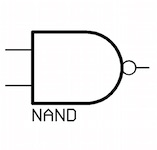
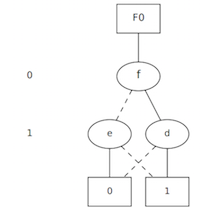
BDD for an NAND

For the NAND Boolean function, we use Cudd_bddNand
The following fragment of code illustrates how to build the BDD for the function f = ¬ (x1 ∧ x2)

Sample program for the OR Boolean function

The main function looks like this

int main (int argc, char *argv[])
{
    char filename[30];
    DdManager *gbm; /* Global BDD manager. */
    gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0); /* Initialize a new BDD manager. */
    DdNode *bdd, *x1, *x2;
    x1 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x1*/
    x2 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x2*/
    bdd = Cudd_bddNand(gbm, x1, x2); /*Perform NAND Boolean operation*/
    Cudd_Ref(bdd);          /*Update the reference count for the node just created.*/
    bdd = Cudd_BddToAdd(gbm, bdd); /*Convert BDD to ADD for display purpose*/
    print_dd (gbm, bdd, 2,4);   /*Print the dd to standard output*/
    sprintf(filename, "./bdd/graph.dot"); /*Write .dot filename to a string*/
    write_dd(gbm, bdd, filename);  /*Write the resulting cascade dd to a file*/
    Cudd_Quit(gbm);
    return 0; 
}

BDD for the NOR Boolean function

The truth table for an NOR

x1	x2	f
0	0	1
0	1	0
1	0	0
1	1	0

Logic gate for an NOR

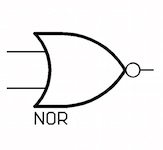
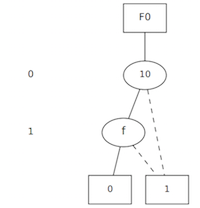
BDD for an NOR

For the NOR Boolean function, we use Cudd_bddNor
The following fragment of code illustrates how to build the BDD for the function f = ¬ (x1 ∨ x2)

Sample program for the NOR Boolean function

The main function looks like this

int main (int argc, char *argv[])
{
    char filename[30];
    DdManager *gbm; /* Global BDD manager. */
    gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0); /* Initialize a new BDD manager. */
    DdNode *bdd, *x1, *x2;
    x1 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x1*/
    x2 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x2*/
    bdd = Cudd_bddNor(gbm, x1, x2); /*Perform NOR Boolean operation*/
    Cudd_Ref(bdd);          /*Update the reference count for the node just created.*/
    bdd = Cudd_BddToAdd(gbm, bdd); /*Convert BDD to ADD for display purpose*/
    print_dd (gbm, bdd, 2,4);   /*Print the dd to standard output*/
    sprintf(filename, "./bdd/graph.dot"); /*Write .dot filename to a string*/
    write_dd(gbm, bdd, filename);  /*Write the resulting cascade dd to a file*/
    Cudd_Quit(gbm);
    return 0; 
}

BDD for the NOT Boolean function

The truth table for a NOT

x1	f
0	1
1	0

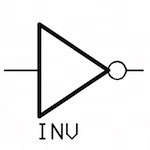
Logic gate for a NOT

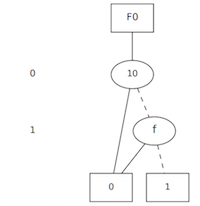
BDD for a NOT

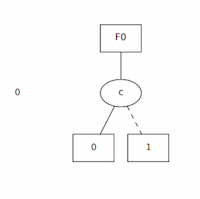
For the NOT Boolean function, we use Cudd_Not
The following fragment of code illustrates how to build the BDD for the function f = ¬x1

Sample program for the NOT Boolean function

The main function looks like this

int main (int argc, char *argv[])
{
    char filename[30];
    DdManager *gbm; /* Global BDD manager. */
    gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0); /* Initialize a new BDD manager. */
    DdNode *bdd, *x1;
    x1 = Cudd_bddNewVar(gbm); /*Create a new BDD variable x1*/
    bdd = Cudd_Not(x1); /*Perform NOT Boolean operation*/
    Cudd_Ref(bdd);          /*Update the reference count for the node just created.*/
    bdd = Cudd_BddToAdd(gbm, bdd); /*Convert BDD to ADD for display purpose*/
    print_dd (gbm, bdd, 2,4);   /*Print the dd to standard output*/
    sprintf(filename, "./bdd/graph.dot"); /*Write .dot filename to a string*/
    write_dd(gbm, bdd, filename);  /*Write the resulting cascade dd to a file*/
    Cudd_Quit(gbm);
    return 0;
}

BDD for the function f = x0’x1’x2’x3′

The truth table for this function is the following:

The truth table for f = x0’x1’x2’x3′

x0	x1	x2	x3	f
0	0	0	0	1
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	0
1	1	0	1	0
1	1	1	0	0
1	1	1	1	0

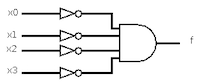
Logic circuit for f = x0’x1’x2’x3′

BDD for f = x0’x1’x2’x3′

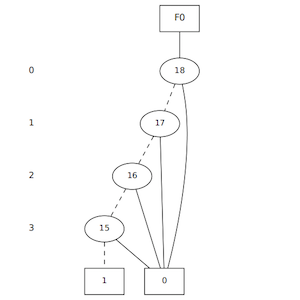
Sample program to create a BDD for the function f = x0’x1’x2’x3′

The entire program looks like this

/*
* FILENAME: tutorial.c
* Overview: BDD tutorial
* AUTHOR: David Kebo Houngninou
*/

#include <sys/types.h>
#include <sys/time.h>
#include <stdio.h>
#include <string.h>
#include <time.h>
#include <math.h>
#include <stdlib.h>
#include "cudd.h"

/**
 * Print a dd summary
 * pr = 0 : prints nothing
 * pr = 1 : prints counts of nodes and minterms
 * pr = 2 : prints counts + disjoint sum of product
 * pr = 3 : prints counts + list of nodes
 * pr > 3 : prints counts + disjoint sum of product + list of nodes
 * @param the dd node
 */
void print_dd (DdManager *gbm, DdNode *dd, int n, int pr )
{
    printf("DdManager nodes: %ld | ", Cudd_ReadNodeCount(gbm)); /*Reports the number of live nodes in BDDs and ADDs*/
    printf("DdManager vars: %d | ", Cudd_ReadSize(gbm) ); /*Returns the number of BDD variables in existence*/
    printf("DdManager reorderings: %d | ", Cudd_ReadReorderings(gbm) ); /*Returns the number of times reordering has occurred*/
    printf("DdManager memory: %ld \n", Cudd_ReadMemoryInUse(gbm) ); /*Returns the memory in use by the manager measured in bytes*/
    Cudd_PrintDebug(gbm, dd, n, pr);  // Prints to the standard output a DD and its statistics: number of nodes, number of leaves, number of minterms.
}


/**
 * Writes a dot file representing the argument DDs
 * @param the node object
 */
void write_dd (DdManager *gbm, DdNode *dd, char* filename)
{
    FILE *outfile; // output file pointer for .dot file
    outfile = fopen(filename,"w");
    DdNode **ddnodearray = (DdNode**)malloc(sizeof(DdNode*)); // initialize the function array
    ddnodearray[0] = dd;
    Cudd_DumpDot(gbm, 1, ddnodearray, NULL, NULL, outfile); // dump the function to .dot file
    free(ddnodearray);
    fclose (outfile); // close the file */
}

int main (int argc, char *argv[])
{
    char filename[30];
    DdManager *gbm; /* Global BDD manager. */
    gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0); /* Initialize a new BDD manager. */
    DdNode *bdd, *var, *tmp_neg, *tmp;
    int i;
    bdd = Cudd_ReadOne(gbm); /*Returns the logic one constant of the manager*/
    Cudd_Ref(bdd); /*Increases the reference count of a node*/
    
    for (i = 3; i >= 0; i--) {
      var = Cudd_bddIthVar(gbm,i); /*Create a new BDD variable*/
      tmp_neg = Cudd_Not(var); /*Perform NOT Boolean operation*/
      tmp = Cudd_bddAnd(gbm, tmp_neg, bdd); /*Perform AND Boolean operation*/
      Cudd_Ref(tmp);
      Cudd_RecursiveDeref(gbm,bdd);
      bdd = tmp;
    }
    
    bdd = Cudd_BddToAdd(gbm, bdd); /*Convert BDD to ADD for display purpose*/
    print_dd (gbm, bdd, 2,4); /*Print the dd to standard output*/
    sprintf(filename, "./bdd/graph.dot"); /*Write .dot filename to a string*/
    write_dd(gbm, bdd, filename);  /*Write the resulting cascade dd to a file*/
    Cudd_Quit(gbm);
    return 0; 
}

Download Tutorial 2

You can download the full code for this example here:

tutorial2.tar.gz

Tutorial 3: Variable reordering

The purpose of variable reordering is to reduce the size (number of nodes) of the BDD by optimizing the order of the variables. Finding an optimal order for a BDD is an NP-complete problem; therefore, several heuristic methods were developed for variable ordering. The CUDD package provides a rich set of dynamic reordering algorithms that you can apply to your BDD.

After initializing the BDD manager, we can make a call to a variable reordering method (Choose only one of the options below)

// Initialize a new BDD manager
gbm = Cudd_Init(0,0,CUDD_UNIQUE_SLOTS,CUDD_CACHE_SLOTS,0);

//Option 1: Dynamic reordering by sifting
Cudd_AutodynEnable(gbm, CUDD_REORDER_SYMM_SIFT);
Cudd_ReduceHeap(gbm, CUDD_REORDER_SYMM_SIFT, 3000);

//Option 2: Dynamic reordering by window permutation
Cudd_AutodynEnable(gbm, CUDD_REORDER_WINDOW2);
Cudd_ReduceHeap(gbm, CUDD_REORDER_WINDOW2, 3000);

//Option 3: Dynamic reordering by simulated annealing
Cudd_AutodynEnable(gbm, CUDD_REORDER_ANNEALING);
Cudd_ReduceHeap(gbm, CUDD_REORDER_ANNEALING, 3000);

//Option 4: Dynamic reordering by genetic algorithm
Cudd_AutodynEnable(gbm, CUDD_REORDER_GENETIC);
Cudd_ReduceHeap(gbm, CUDD_REORDER_GENETIC, 3000);

//Option 5: Dynamic reordering by swapping
Cudd_AutodynEnable(gbm, CUDD_REORDER_RANDOM);
Cudd_ReduceHeap(gbm, CUDD_REORDER_RANDOM, 3000);

//Option 6: No reordering
Cudd_AutodynDisable (gbm);

Tutorial 4: Additional functions

Algebraic Decision Diagram (ADD) for a fanout

The fanout of a logic gate output is the number of gate inputs it can feed. A fanout can also be modeled as a Boolean function

An Algebraic Decision Diagram (ADD) is a BDD with a set of constant values different than the set {0,1}.
Instead of using a BDD, we use an ADD to represent a fanout because the leaf nodes have values different than 0 and 1.

The truth table for a fanout

x	f1	f2
0	0	0
1	1	1

Representation of a fanout

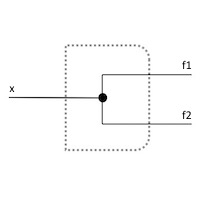
ADD for a fanout

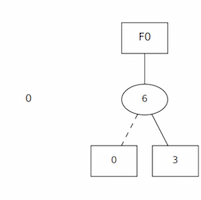
/**Function********************************************************************

  Synopsis    [Create a ADD from different sizes of fanouts]

  Description [The Else branch is always a zero (0)
 	Depending on the number of fanouts the Then branch varies between: (3 or 7 or 15 or 31 etc.)]

  @param the number of fanout branches
******************************************************************************/
DdNode * Cudd_fanout (int fanouts)
{
    DdNode *var = Cudd_addNewVar(gbm); /*Root node of the fanout*/
    Cudd_Ref(var);
    int coef = pow(2, fanouts)-1; /*Calculate the max value depending on the number of fanouts*/
    DdNode *retval = Cudd_addIte(gbm, var,  Cudd_addConst (gbm, (CUDD_VALUE_TYPE)coef), Cudd_addConst(gbm, (CUDD_VALUE_TYPE)0)); /*Else branch=0, Then branch=(3 or 7 or 15 or 31 etc.)*/
    Cudd_RecursiveDeref(gbm,var);
    return retval;
}

Algebraic Decision Diagram (ADD) for a crossover

A crossover represents two wires crossing each other. A crossover can also be modeled as a Boolean function

An Algebraic Decision Diagram (ADD) is a BDD with a set of constant values different than the set {0,1}.
Instead of using a BDD, we use an ADD to represent a crossover because the leaf nodes have values different than 0 and 1.

The truth table for a crossover

x1	x2	f1	f2
0	0	0	0
0	1	1	0
1	0	0	1
1	1	1	1

Representation of a crossover

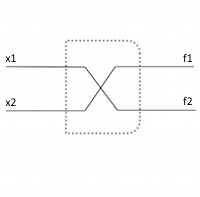
ADD for a crossover

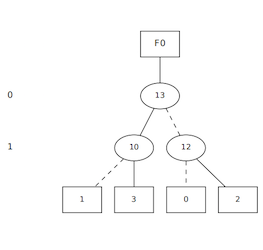
/**Function********************************************************************

  Synopsis    [Creates a ADD for a crossover]

  Description [A crossover is the intersection (crossing) of two wires
  The terminal nodes of a crossover ADD are 0, 2, 1 and 3]

  @param none
******************************************************************************/
DdNode * Cudd_crossover ()
{
    DdNode *var1 = Cudd_addNewVar(gbm); /*First variable in the crossover DD*/
    Cudd_Ref(var1);
    DdNode *var2 = Cudd_addNewVar(gbm); /*Second variable in the crossover DD*/
    Cudd_Ref(var2);
    DdNode *node1 = Cudd_addIte(gbm,var2, Cudd_addConst (gbm, (CUDD_VALUE_TYPE)2), Cudd_addConst(gbm, (CUDD_VALUE_TYPE)0)); /*Else branch=0, Then branch=2*/
    Cudd_Ref(node1);
    DdNode *node2 = Cudd_addIte(gbm,var2, Cudd_addConst (gbm, (CUDD_VALUE_TYPE)3), Cudd_addConst(gbm, (CUDD_VALUE_TYPE)1)); /*Else branch=1, Then branch=3*/
    Cudd_Ref(node2);

    DdNode *retval = Cudd_addIte(gbm,var1, node2 ,node1);
    Cudd_RecursiveDeref(gbm,var1);
    Cudd_RecursiveDeref(gbm,var2);
    Cudd_RecursiveDeref(gbm,node1);
    Cudd_RecursiveDeref(gbm,node2);
    return retval;
}

Learn it by examples

By David Kebo Houngninou

Table of contents

What is CUDD?

Where to download CUDD?

How to install CUDD?

Tutorial 1: Write your first program with CUDD

Sample code for the main program

How to debug your program

Sample function for printing a DD summary

Visualize the BDD

Sample function for printing a dd summary

Sample program for printing a creating and printing a dd (Complete)

Graph representation of the BDD

Download Tutorial 1

Tutorial 2: BDD of Boolean functions

BDD for the Exclusive-OR Boolean function

The truth table for an Exclusive-OR

Logic gate for an Exclusive-OR

BDD for an Exclusive-OR

Sample program for the XOR Boolean function

BDD for the AND Boolean function

The truth table for an AND

Logic gate for a logic AND

BDD for a logic AND

Sample program for the AND Boolean function

BDD for the OR Boolean function

The truth table for a logic OR

Logic gate for a logic OR

BDD for a logic OR

Sample program for the OR Boolean function

BDD for the XNOR Boolean function

The truth table for an XNOR

Logic gate for an XNOR

BDD for an XNOR

Sample program for the XNOR Boolean function

BDD for the NAND Boolean function

The truth table for an NAND

Logic gate for an NAND

BDD for an NAND

Sample program for the OR Boolean function

BDD for the NOR Boolean function

The truth table for an NOR

Logic gate for an NOR

BDD for an NOR

Sample program for the NOR Boolean function

BDD for the NOT Boolean function

The truth table for a NOT

Logic gate for a NOT

BDD for a NOT

Sample program for the NOT Boolean function

BDD for the function f = x0’x1’x2’x3′

The truth table for f = x0’x1’x2’x3′

Logic circuit for f = x0’x1’x2’x3′

BDD for f = x0’x1’x2’x3′

Sample program to create a BDD for the function f = x0’x1’x2’x3′

Download Tutorial 2

Tutorial 3: Variable reordering

Tutorial 4: Additional functions

Algebraic Decision Diagram (ADD) for a fanout

The truth table for a fanout

Representation of a fanout

ADD for a fanout

Algebraic Decision Diagram (ADD) for a crossover

The truth table for a crossover

Representation of a crossover

ADD for a crossover